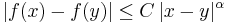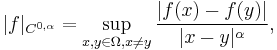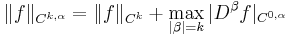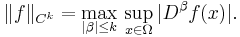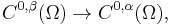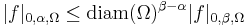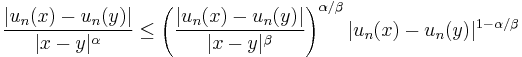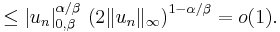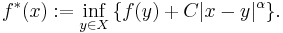Hölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C,  , such that
, such that
for all x and y in the domain of ƒ. More generally, the condition can be formulated for functions between any two metric spaces. The number  is called the exponent of the Hölder condition. If
is called the exponent of the Hölder condition. If  = 1, then the function satisfies a Lipschitz condition. If
= 1, then the function satisfies a Lipschitz condition. If  = 0, then the function simply is bounded. The condition is named after Otto Hölder.
= 0, then the function simply is bounded. The condition is named after Otto Hölder.
Contents |
Hölder spaces
Hölder spaces consisting of functions satisfying a Hölder condition are basic in areas of functional analysis relevant to solving partial differential equations, and in dynamical systems. The Hölder space 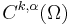 , where
, where  is an open subset of some Euclidean space and k ≥ 0 an integer, consists of those functions on
is an open subset of some Euclidean space and k ≥ 0 an integer, consists of those functions on  having continuous derivatives up to order k and such that the kth partial derivatives are Hölder continuous with exponent
having continuous derivatives up to order k and such that the kth partial derivatives are Hölder continuous with exponent  , where 0 <
, where 0 <  ≤ 1. This is a locally convex topological vector space. If the Hölder coefficient
≤ 1. This is a locally convex topological vector space. If the Hölder coefficient
is finite, then the function ƒ is said to be (uniformly) Hölder continuous with exponent  in
in  . In this case, Hölder coefficient serves as a seminorm. If the Hölder coefficient is merely bounded on compact subsets of Ω, then the function ƒ is said to be locally Hölder continuous with exponent α in Ω.
. In this case, Hölder coefficient serves as a seminorm. If the Hölder coefficient is merely bounded on compact subsets of Ω, then the function ƒ is said to be locally Hölder continuous with exponent α in Ω.
If the function ƒ and its derivatives up to order k are bounded on the closure of Ω, then the Hölder space 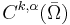 can be assigned the norm
can be assigned the norm
where β ranges over multi-indices and
These norms and seminorms are often denoted simply 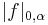 and
and 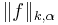 or also
or also 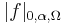 and
and 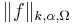 in order to stress the dependence on the domain of f. If
in order to stress the dependence on the domain of f. If  is open and bounded, then
is open and bounded, then 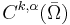 is a Banach space with respect to the norm
is a Banach space with respect to the norm 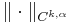 .
.
Compact embedding of Hölder spaces
Let Ω be a bounded subset of some Euclidean space (or more generally, any totally bounded metric space) and let 0 < α < β ≤ 1 two Hölder exponents. Then, there is an obvious inclusion of the corresponding Hölder spaces:
which is continuous since, by definition of the Hölder norms, the inequality
holds for all 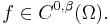 Moreover, this inclusion is compact, meaning that bounded sets in the
Moreover, this inclusion is compact, meaning that bounded sets in the 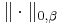 norm are relatively compact in the
norm are relatively compact in the 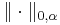 norm. This is a direct consequence of the Ascoli-Arzelà theorem. Indeed, let
norm. This is a direct consequence of the Ascoli-Arzelà theorem. Indeed, let 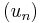 be a bounded sequence in
be a bounded sequence in 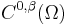 . Thanks to the Ascoli-Arzelà theorem we can assume without loss of generality that
. Thanks to the Ascoli-Arzelà theorem we can assume without loss of generality that  uniformly, and we can also assume
uniformly, and we can also assume 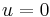 . Then
. Then 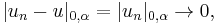 because
because
Examples
- If 0 < α ≤ β ≤ 1 then all
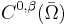 Hölder continuous functions on a bounded set
Hölder continuous functions on a bounded set  are also
are also 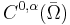 Hölder continuous. This also includes β = 1 and therefore all Lipschitz continuous functions on a bounded set are also
Hölder continuous. This also includes β = 1 and therefore all Lipschitz continuous functions on a bounded set are also 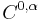 Hölder continuous.
Hölder continuous.
- The function
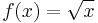 defined on [0, 1] is not Lipschitz continuous, but is
defined on [0, 1] is not Lipschitz continuous, but is 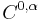 Hölder continuous for α ≤ 1/2.
Hölder continuous for α ≤ 1/2.
- In the same manner, the function
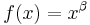 (with β ≤1) defined on [0, 1] serves as a prototypical example of a function that is
(with β ≤1) defined on [0, 1] serves as a prototypical example of a function that is 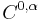 Hölder continuous for 0 < α ≤ β, but not for α > β.
Hölder continuous for 0 < α ≤ β, but not for α > β.
- There are examples of uniformly continuous functions that are not α–Hölder continuous for any α. For instance, the function defined on [0,1/2] by
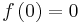 and by
and by 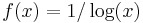 otherwise is continuous, and therefore uniformly continuous. It does not satisfy a Hölder condition of any order, however.
otherwise is continuous, and therefore uniformly continuous. It does not satisfy a Hölder condition of any order, however.
- For α > 1, any α–Hölder continuous function on [0, 1] is a constant.
- Peano curves from [0, 1] onto the square [0, 1]2 can be constructed to be 1/2–Hölder continuous. It can be proved that when α > 1/2, the image of a α–Hölder continuous function from the unit interval to the square cannot fill the square.
- A closed additive subgroup of an infinite dimensional Hilbert space H, connected by α–Hölder continuous arcs with α > 1/2, is a linear subspace. There are closed additive subgroups of H, not linear subspaces, connected by 1/2–Hölder continuous arcs. An example is the additive subgroup
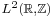 of the Hilbert space
of the Hilbert space 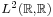 .
.
- Any α–Hölder continuous function
 on a metric space
on a metric space  admits a Lipschitz approximation by means of a sequence of functions
admits a Lipschitz approximation by means of a sequence of functions 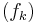 such that
such that 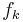 is
is  -Lipschitz and
-Lipschitz and 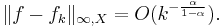 Conversely, any such sequence
Conversely, any such sequence 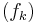 of Lipschitz functions converges to an α–Hölder continuous uniform limit
of Lipschitz functions converges to an α–Hölder continuous uniform limit  .
.
- Any α–Hölder function
 on a subset
on a subset  of a normed space
of a normed space  admits a uniformly continuous extension to the whole space, which is Hölder continuous with the same constant C and the same exponent α. The larger such extension is:
admits a uniformly continuous extension to the whole space, which is Hölder continuous with the same constant C and the same exponent α. The larger such extension is:
- Functions in Sobolev space can be embedded into the appropriate Hölder space via Morrey's inequality if the spatial dimension is less than the exponent of the Sobolev space. To be precise, if n < p ≤ ∞ then there exists a constant C, depending only on p and n, such that
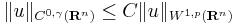 for all u ∈ C1 (Rn) ∩ Lp(Rn), where
for all u ∈ C1 (Rn) ∩ Lp(Rn), where 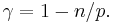 Thus if u ∈ W1,p(Rn), then u is in fact Hölder continuous of exponent γ, after possibly being redefined on a set of measure 0.
Thus if u ∈ W1,p(Rn), then u is in fact Hölder continuous of exponent γ, after possibly being redefined on a set of measure 0.
- Functions which are locally integrable and whose integrals satisfy an appropriate growth condition are also Hölder continuous. For example, if we let
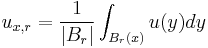 and u satisfies
and u satisfies 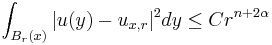 , then u is Hölder continuous with exponent
, then u is Hölder continuous with exponent  .[1]
.[1]
- Functions whose oscillation decay at a fixed rate with respect to distance are Hölder continuous with an exponent that is determined by the rate of decay. For instance, if
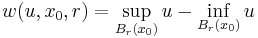 for some function
for some function 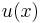 satisfies
satisfies 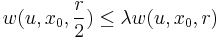 for a fixed
for a fixed  with
with 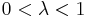 and all sufficiently small values of r, then u is Hölder continuous.
and all sufficiently small values of r, then u is Hölder continuous.
Note
- ^ See, for example, Han and Lin, Chapter 3, Section 1. This result was originally due to Sergio Campanato.
References
- Lawrence C. Evans (1998). Partial Differential Equations. American Mathematical Society, Providence. ISBN 0-8218-0772-2.
- Gilbarg, D.; Trudinger, Neil (1983). Elliptic Partial Differential Equations of Second Order. New York: Springer. ISBN 3-540-41160-7..
- Han, Qing; Lin, Fanghua (1997). Elliptic Partial Differential Equations. New York: Courant Institute of Mathematical Sciences. ISBN 0965870308. OCLC 38168365 MR1669352